两个矩形信号做卷积——不经意的小问题

dinosaur

两个相同的矩形信号做卷积 / Convolution of two identical rectangular signals

背景

晚上做信号与系统习题的时候，遇到了一个卷积计算的问题，发现在我对它的理解出现了一点奇妙的偏差，通过网络费了好些功夫才梳理通。理解以后，就想写一篇博文记录下这一问题，希望能给大家一点帮助，~~顺便防止我以后又忘记了~~。

问题

题目要求的计算过程中，有计算如下两个相同矩形脉冲信号的卷积：

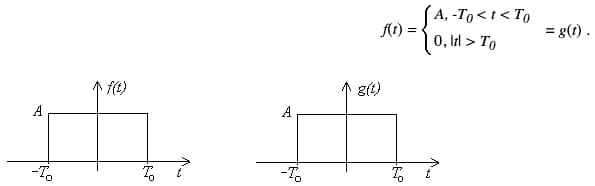rectangular-signals 图一，取自参考链接[1]

虽然我知道它的结果，是一个如下图所示的三角形脉冲信号——课上与书上都是这么说的：

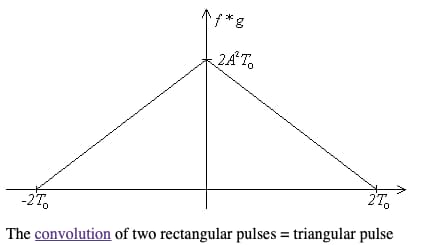triangular-pulse 图二，同样取自参考链接[1]

可是由于没有给过程，所以我想不到正确的计算方式是什么，也就无从改错。

思路

由上述可知，有两个相同的矩形脉冲信号可表示为：

$$ \tag{1.1} f(x) = \begin{cases} A, &\text{if } ~ {-T_0 \lt t \lt T_0} \\ 0, &\text{if } ~ {|t| ~ \gt T_0} \end{cases} ~ = ~ g(t) $$

而当信号相互卷积时，连续时间下，由卷积积分的公式：

$$ \tag{1.2} y(t) = \int_{-\infty}^{+\infty}{x(\tau)}{h(t-\tau)}{\rm d}{\tau} ~ = ~ x(t){\ast}h(t) $$

两者相卷积时，在图解时可将相应沿$y$轴翻转，然后左移一定的距离直到两个信号不再重叠，再逐渐右移，重叠后逐点计算卷积值。（详细的计算过程默认读者已经了解，如不了解可参见奥本海姆的《信号与系统》第二章）

而在此处，由于两个信号相同，所以其卷积可写为$y(t) = x(t){\ast}x(t)$，任选其一作信号的响应$x_2(t)$，故其沿$y$轴反转后保持不变，在左移没有重复区域后再次右移的过程中，与信号$x_1(t)$最早相接触的地方应该是$t = -T_0$的时候，而正确的结果应该是$t = -2T_0$。

Obviously，肯定有地方出了问题。

纠错

回顾之前做的例题中，其响应一般都是从零点开始的，从来没有从$t \lt 0$的情况；且当两个矩形脉冲信号都是从$t = 0$开始时，我可以计算得到正确的输出，为一个从$t = 0$到$t = 4T_0$类似图二的三角形，所以肯定是因为我对响应处理不当而产生的错误。

为此，我翻书想看看有没有相似的例题，无果，随后上万能的Google试试能不能搜到相似情况的解析。中文搜索出来全都是CSDN或者博客园的雷同文章，一点帮助都没有……换了英文关键词后，找到了后面参考栏里的两个网页，看后我知道是哪里出错了：

首先由题意，作出方程：

$$ \tag{2.1} y(t) = \int_{-\infty}^{+\infty}{x_1(\tau)}{x_2(t-\tau)}{\rm d}{\tau} $$

由图解法可作出下图：

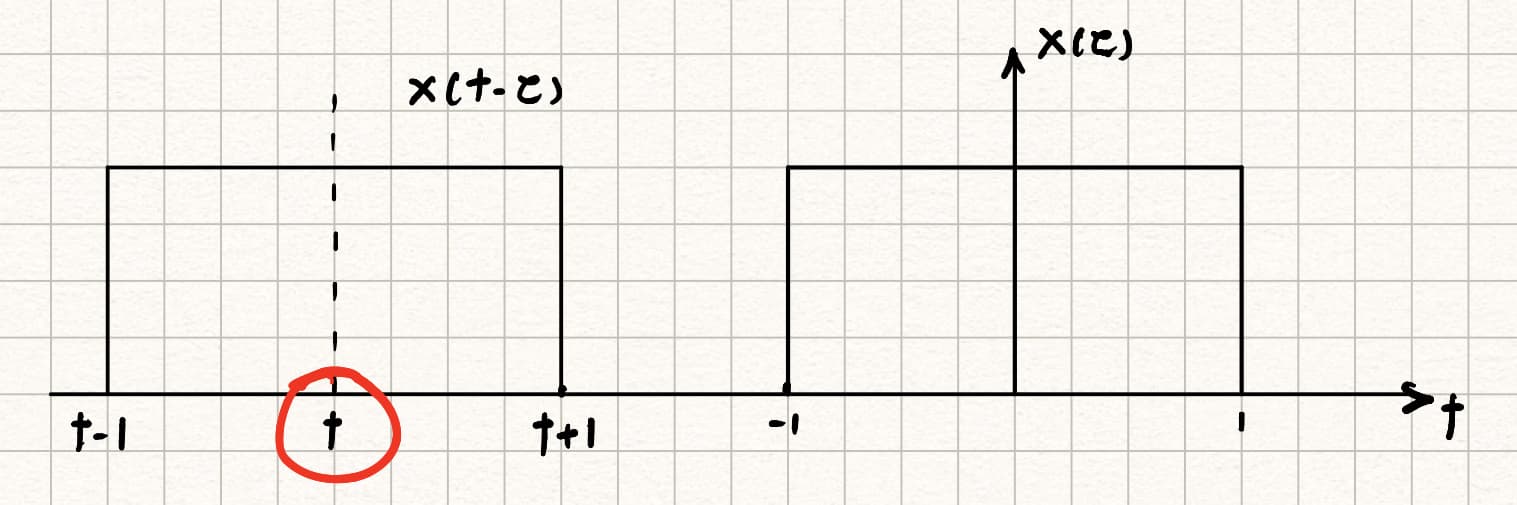
注意：响应$x_2(t)$与输入信号$x_1(t)$相乘积分的结果在$t = t$的时候，而不是$t = t + 1$处，这是关键的一步。之前我的错误就是将其积分之和误放在了$t = t + 1$的地方，导致输出信号开始于$t + 1$而不是$t$。

之后便一帆风顺了。究其错误原因：我之所以会那样计算，首先是先入为主，认为之前都是从响应重叠的地方开始，想必这次也应该是这样；其次是对概念的理解较为薄弱：$h(t - \tau)$代表了在$t = \tau$处一个时移后的脉冲信号$\delta(0)$的响应，因此$x_2(t-\tau)$也应该代表在$t = \tau$处一个时移后的脉冲信号$\delta(0)$的响应，其响应在$t$处，而非最右端$t+1$处。

图像得到了，至于解析式的结果，我也一并附在这里吧：

$$ \begin{split} x_1(t)*x_2(t) &= {\int_{-\infty}^{+\infty}{x_1(\tau)}{x_2(t-\tau)}{\rm d}{\tau}} \\ &=\begin{cases} {\int_{-T_0}^{t+T_0}1{\cdot}1{\rm d}{\tau}}, &\text{if } ~ {-2T_0 \lt t \lt 0} \\ {\int_{t-T_0}^{T_0}1{\cdot}1{\rm d}{\tau}}, &\text{if } ~ {0 \lt t \lt 2T_0} \end{cases} \\ &=\begin{cases} {t+2T_0}, &\text{if } ~ {-2T_0 \lt t \lt 0} \\ {2T_0-t}, &\text{if } ~ {0 \lt t \lt 2T_0} \\ {0}, , &\text{if } ~ {|t| \gt 2T_0} \end{cases} \end{split}\tag{2.2} $$

大概就是这样了，如果感觉理解起来有些困难的话，推荐大家看看第二个链接中的YouTube视频，情况不完全相同，不过Adam小哥讲得超棒的！